Fungsi linear adalah materi aljabar yang membahas hubungan dua variabel yang dinyatakan dalam bentuk persamaan garis lurus. Dalam konsep ini, gradien menunjukkan arah dan tingkat kemiringan garis, sedangkan konstanta menentukan titik perpotongan dengan sumbu-Y. Pemahaman fungsi linear sangat penting karena sering digunakan untuk menggambarkan hubungan yang bersifat tetap dan teratur, seperti pertumbuhan tabungan, perhitungan biaya, atau hubungan jarak dan waktu.

Mempelajari soal fungsi linear membantu Anda memahami pola perubahan secara logis, menyusun model matematika dari suatu informasi, serta menafsirkan grafik dengan lebih tepat. Materi ini kerap muncul dalam berbagai bentuk soal, mulai dari substitusi nilai, menentukan persamaan garis, hingga analisis grafik dan soal cerita berbasis konteks.

Kisi-Kisi Soal Fungsi Linear Terbaru

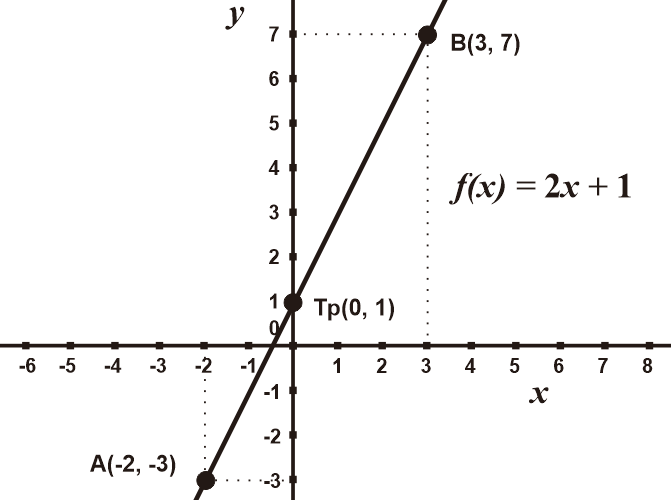
Kisi-kisi ini disusun untuk mengarahkan fokus belajar pada kemampuan utama, seperti menghitung nilai fungsi, menentukan gradien, menyusun persamaan dari satu atau dua titik, serta menganalisis hubungan antar garis. Dengan memahami ruang lingkup ini, Anda dapat mengerjakan soal fungsi linear dengan lebih terstruktur dan percaya diri.

1. Menentukan Nilai Fungsi Linear

Menentukan nilai fungsi linear untuk nilai variabel tertentu.

2. Menentukan Bentuk Fungsi Linear

Menentukan bentuk fungsi linear berdasarkan informasi yang diberikan.

3. Menentukan Gradien Fungsi Linear

Menentukan besar gradien suatu fungsi linear dari data atau dua titik yang diketahui.

4. Menentukan Titik Potong dengan Sumbu

Menentukan titik potong fungsi linear terhadap sumbu koordinat.

5. Menentukan Persamaan Fungsi Linear dari Dua Titik

Menentukan persamaan fungsi linear berdasarkan dua titik yang diketahui.

6. Menentukan Persamaan Fungsi Linear dari Gradien dan Satu Titik

Menentukan persamaan fungsi linear berdasarkan gradien dan satu titik yang diketahui.

7. Menentukan Grafik Fungsi Linear

Menentukan atau mengenali grafik fungsi linear dari informasi yang tersedia.

8. Menentukan Hubungan Antar Dua Fungsi Linear

Menentukan hubungan dua fungsi linear berdasarkan gradien atau posisi grafiknya.

9. Menentukan Titik Potong Dua Fungsi Linear

Menentukan titik perpotongan dua fungsi linear yang diberikan.

10. Penerapan Fungsi Linear dalam Masalah Kontekstual

Menentukan besaran yang diminta pada permasalahan nyata yang dapat dimodelkan dengan fungsi linear.

Contoh Soal Fungsi Linear + Kunci Jawaban & Pembahasan

Contoh soal fungsi linear disusun untuk membantu Anda memahami penerapan konsep persamaan garis lurus dalam berbagai situasi. Melalui latihan yang disertai pembahasan jelas, Anda dapat berlatih menentukan nilai fungsi, mencari gradien, menyusun persamaan garis, serta menyelesaikan permasalahan secara sistematis dan akurat.

Soal 1

Sebuah perusahaan jasa desain grafis menetapkan biaya pembuatan logo dengan model fungsi f(x) = 150.000x + 200.000, dengan x menyatakan jumlah revisi tambahan yang diminta klien. Jika seorang klien meminta 3 kali revisi tambahan, berapakah total biaya yang harus dibayarkan?

A. Rp500.000
B. Rp550.000
C. Rp600.000
D. Rp650.000
E. Rp700.000

Jawaban: D

Pembahasan:
Substitusi x = 3
f(3) = 150.000(3) + 200.000
= 450.000 + 200.000
= 650.000

Soal 2

Diketahui fungsi linear ( f(x) = 4x – 9 ).
Tentukan nilai ( f(-3) ).

A. −21
B. −18
C. −15
D. −12
E. −9

Jawaban: A

Pembahasan:
f(-3) = 4(-3) − 9
= −12 − 9
= −21

Soal 3

Suatu garis memiliki gradien 6 dan memotong sumbu-Y di titik (0, −4).
Persamaan garis tersebut adalah …

A. y = 6x − 4
B. y = 6x + 4
C. y = −6x − 4
D. y = −6x + 4
E. y = 4x − 6

Jawaban: A

Pembahasan:
Bentuk umum fungsi linear: y = mx + c
m = 6 dan c = −4
Sehingga persamaan garisnya adalah
y = 6x − 4

Soal 4

Suatu garis melalui titik (1, 5) dan (3, 9). Tentukan persamaan garis tersebut.

A. y = 2x + 3
B. y = 3x + 2
C. y = 2x + 1
D. y = 4x + 1
E. y = x + 4

Jawaban: A

Pembahasan:
Gradien:
m = (9 − 5) / (3 − 1)
= 4 / 2
= 2

Gunakan titik (1,5):
y − 5 = 2(x − 1)
y − 5 = 2x − 2
y = 2x + 3

Soal 5

Garis melalui titik (2, −1) dan (6, 7). Gradien garis tersebut adalah …

A. 1
B. 2
C. 3
D. 4
E. 5

Jawaban: B

Pembahasan:
m = (7 − (−1)) / (6 − 2)
= 8 / 4
= 2

Soal 6

Gradien dari persamaan 3x − 2y = 6 adalah …

A. −3/2
B. 3/2
C. −2/3
D. 2/3
E. 1

Jawaban: B

Pembahasan:
Ubah ke bentuk y = mx + c

3x − 2y = 6
−2y = −3x + 6
y = (3/2)x − 3

Gradien = 3/2

Soal 7

Tentukan titik potong dengan sumbu-X dari persamaan
y = 5x − 10.

A. (1,0)
B. (2,0)
C. (3,0)
D. (4,0)
E. (5,0)

Jawaban: B

Pembahasan:
Titik potong sumbu-X saat y = 0

0 = 5x − 10
5x = 10
x = 2

Titiknya adalah (2,0)

Soal 8

Diketahui persamaan y = −3x + 9.
Titik potong dengan sumbu-Y adalah …

A. (0,3)
B. (0,6)
C. (0,9)
D. (9,0)
E. (−9,0)

Jawaban: C

Pembahasan:
Saat x = 0
y = −3(0) + 9 = 9
Titiknya (0,9)

Soal 9

Gradien suatu garis adalah −2 dan melalui titik (1, 4). Persamaan garis tersebut adalah …

A. y = −2x + 6
B. y = −2x + 4
C. y = 2x − 6
D. y = 2x + 6
E. y = −2x − 6

Jawaban: A

Pembahasan:
Gunakan rumus titik-gradien:

y − 4 = −2(x − 1)
y − 4 = −2x + 2
y = −2x + 6

Soal 10

Grafik fungsi y = −4x + 2 memiliki ciri …

A. Garis naik dan memotong sumbu-Y di 2
B. Garis turun dan memotong sumbu-Y di 2
C. Garis naik dan memotong sumbu-Y di −2
D. Garis sejajar sumbu-X
E. Garis vertikal

Jawaban: B
Pembahasan:
Gradien negatif (−4) → grafik menurun
Konstanta 2 → memotong sumbu-Y di 2

Soal 11

Sebuah garis melalui titik (−2, 1) dan (4, 13). Tentukan persamaan garis tersebut.

A. y = 2x + 5
B. y = 3x + 7
C. y = 2x + 3
D. y = 3x + 1
E. y = x + 5

Jawaban: A

Pembahasan:
Gradien:
m = (13 − 1) / (4 − (−2))
= 12 / 6
= 2

Gunakan titik (−2,1):
y − 1 = 2(x + 2)
y − 1 = 2x + 4
y = 2x + 5

Soal 12

Diketahui
f(x) = 4x − 3
g(x) = 4x + 5

Hubungan grafik kedua fungsi tersebut adalah …

A. Berpotongan di satu titik
B. Sejajar
C. Berimpit
D. Tegak lurus
E. Tidak dapat ditentukan

Jawaban: B

Pembahasan:
Gradien f = 4
Gradien g = 4
Gradien sama, konstanta berbeda → sejajar

Soal 13

Diketahui garis
y = 2x + 1
dan
y = −½x + 4

Kedua garis tersebut adalah …

A. Sejajar
B. Berimpit
C. Tegak lurus
D. Berpotongan biasa
E. Tidak berhubungan

Jawaban: C

Pembahasan:
Jika m₁ × m₂ = −1 → tegak lurus

2 × (−½) = −1
Maka garis tegak lurus

Soal 14

Tentukan titik potong garis
y = 3x − 2
dan
y = x + 4.

A. (2,4)
B. (3,7)
C. (1,1)
D. (3,5)
E. (2,5)

Jawaban: B

Pembahasan:
Samakan kedua persamaan:

3x − 2 = x + 4
2x = 6
x = 3

Substitusi:
y = 3(3) − 2
= 9 − 2
= 7

Titik potong = (3,7)

Soal 15

Suatu fungsi linear memiliki gradien negatif dan memotong sumbu-Y di atas titik asal (0,0). Grafik fungsi tersebut akan …

A. Naik dari kiri ke kanan
B. Turun dari kiri ke kanan
C. Sejajar sumbu-X
D. Tegak lurus sumbu-X
E. Tidak memotong sumbu-Y

Jawaban: B

Pembahasan:
Gradien negatif → grafik menurun
Memotong sumbu-Y di atas 0 → konstanta positif

Soal 16

Sebuah percetakan menetapkan biaya tetap Rp500.000 dan biaya tambahan Rp20.000 per buku yang dicetak. Jika x adalah jumlah buku, model fungsi biaya adalah …

A. 20.000x − 500.000
B. 500.000x + 20.000
C. 20.000x + 500.000
D. 520.000x
E. 20.000(x + 500.000)

Jawaban: C

Pembahasan:
Biaya total = biaya variabel + biaya tetap
= 20.000x + 500.000

Soal 17

Seseorang memiliki tabungan awal Rp2.000.000 dan menabung Rp250.000 setiap bulan. Berapa total tabungan setelah 6 bulan?

A. Rp3.000.000
B. Rp3.250.000
C. Rp3.500.000
D. Rp3.750.000
E. Rp4.000.000

Jawaban: C

Pembahasan:
Model: y = 250.000x + 2.000.000

Untuk x = 6:
y = 250.000(6) + 2.000.000
= 1.500.000 + 2.000.000
= 3.500.000

Soal 18

Jika f(x) = 5x − 3 dan diketahui f(x) = 17, maka nilai x adalah …

A. 2
B. 3
C. 4
D. 5
E. 6

Jawaban: C

Pembahasan:
5x − 3 = 17
5x = 20
x = 4

Soal 19

Tentukan titik potong sumbu-X dari persamaan
2x + 5 = 0.

A. (−2,5)
B. (2,−5)
C. (−2.5,0)
D. (2.5,0)
E. (0,−2.5)

Jawaban: C

Pembahasan:
2x = −5
x = −2,5
Titiknya adalah (−2,5 ; 0)

Soal 20

Jika gradien suatu garis diperbesar (nilai positifnya semakin besar), maka grafik akan …

A. Semakin landai
B. Semakin curam
C. Berubah menjadi horizontal
D. Berubah menjadi vertikal
E. Tidak berubah

Jawaban: B

Pembahasan:
Semakin besar gradien positif, semakin besar kenaikan nilai ( y ) untuk setiap kenaikan 1 satuan ( x ). Akibatnya garis menjadi tidak landai, tetapi semakin miring ke atas. Jadi, makin besar nilai gradien, grafik semakin curam naik dari kiri ke kanan.

Ingin Lebih Mudah Menguasai Fungsi Linear melalui Contoh Soal dan Pembahasan Lengkap?

Melalui utbk.or.id, berbagai contoh soal fungsi linear disusun secara bertahap untuk membantu Anda memahami konsep gradien, titik potong, dan persamaan garis dengan lebih jelas. Setiap soal dilengkapi pembahasan runtut dan mudah diikuti, sehingga Anda dapat memahami alur penyelesaian dengan tepat serta lebih percaya diri dalam menghadapi berbagai tipe soal fungsi linear.