Rotasi merupakan salah satu materi transformasi geometri yang membahas perputaran suatu titik atau bangun terhadap pusat tertentu dengan besar sudut tertentu. Konsep ini sering muncul dalam soal matematika karena menguji kemampuan memahami posisi koordinat setelah suatu objek diputar.

Kumpulan soal rotasi ini disusun untuk melatih kemampuan tersebut secara bertahap, mulai dari rotasi sederhana terhadap titik pusat (0,0) hingga rotasi terhadap titik tertentu, sehingga memudahkan memahami konsep tanpa terasa terlalu rumit.

Kisi-Kisi Soal Rotasi

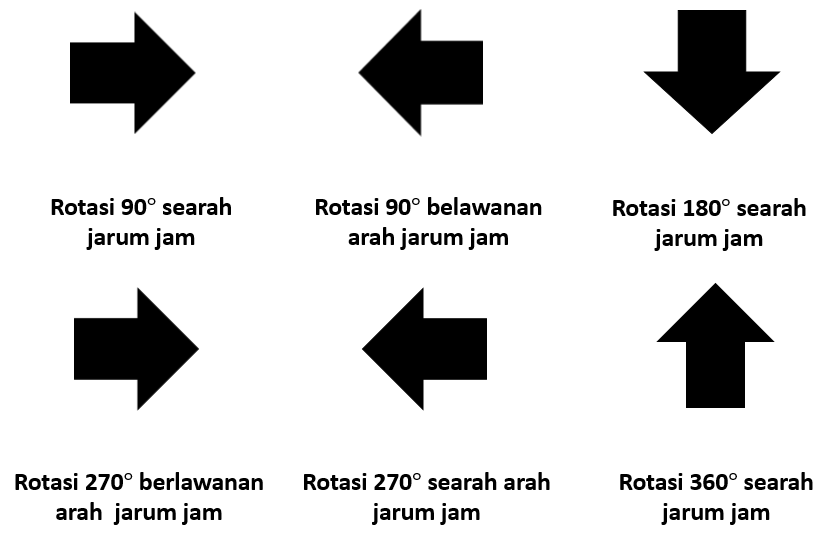
Kisi-kisi rotasi ini disusun agar pemula memiliki panduan jelas tentang materi apa saja yang perlu dipelajari terlebih dahulu. Pembahasan dimulai dari pengertian rotasi, arah putaran searah atau berlawanan jarum jam, hingga penggunaan rumus rotasi pada koordinat.

Dengan mengikuti kisi-kisi ini, proses belajar menjadi lebih terstruktur dan tidak acak. Setiap tahap disusun secara bertahap sehingga lebih mudah dipahami sebelum masuk ke soal yang lebih kompleks.

1. Menentukan Bayangan Titik Hasil Rotasi
Menentukan posisi bayangan suatu titik setelah diputar terhadap pusat tertentu dengan besar sudut tertentu.

2. Menentukan Bayangan Bangun Datar Hasil Rotasi
Menentukan bayangan suatu bangun datar setelah mengalami rotasi.

3. Rotasi terhadap Titik Pusat Koordinat
Menentukan hasil rotasi titik atau bangun dengan pusat rotasi di titik pusat koordinat.

4. Rotasi terhadap Titik Bukan Pusat Koordinat
Menentukan hasil rotasi dengan pusat rotasi berada di titik tertentu selain titik pusat.

5. Menentukan Arah Rotasi
Menentukan hasil rotasi dengan arah searah jarum jam atau berlawanan arah jarum jam.

6. Menentukan Besar Sudut Rotasi
Menentukan besar sudut rotasi berdasarkan posisi titik asal dan bayangannya.

7. Menentukan Posisi Titik Asal dari Bayangan Rotasi
Menentukan posisi titik atau bangun asal jika diketahui hasil rotasinya.

8. Rotasi Berulang
Menentukan hasil rotasi yang dilakukan lebih dari satu kali secara berurutan.

9. Menentukan Kesebangunan Bangun Hasil Rotasi
Menentukan kesesuaian bentuk dan ukuran bangun sebelum dan sesudah rotasi.

10. Penerapan Rotasi dalam Masalah Geometris
Menentukan hasil rotasi pada permasalahan geometri yang melibatkan simetri atau pemetaan bangun.

Contoh Soal Rotasi & Pembahasannya

Contoh soal rotasi disajikan dalam bentuk koordinat titik atau bangun sederhana yang langsung bisa dijadikan bahan latihan. Soal-soal tersebut membantu membiasakan diri memahami perubahan posisi titik setelah rotasi dengan sudut tertentu.

Melalui latihan seperti ini, pemahaman rumus rotasi menjadi lebih konkret karena langsung diterapkan pada perhitungan nyata. 

Soal nomor 1
Titik A berada pada koordinat (4,−2) di bidang Cartesius. Titik tersebut dirotasikan 90° searah jarum jam dengan pusat di titik (0,0).

A. (2,4)
B. (−2,4)
C. (−4,2)
D. (−2,−4)
E. (4,2)

Jawaban: D
Pembahasan: Rotasi 90° searah jarum jam menggunakan rumus (x,y) → (y,−x) sehingga dari (4,−2) diperoleh bayangan (−2,−4).

Soal nomor 2
Titik B terletak pada koordinat (3,5) di bidang koordinat. Titik tersebut diputar 90° berlawanan arah jarum jam dengan pusat (0,0).

A. (−5,3)
B. (5,−3)
C. (3,−5)
D. (−3,−5)
E. (−5,−3)

Jawaban: A
Pembahasan: Rotasi 90° berlawanan arah jarum jam memakai (x,y) → (−y,x) sehingga (3,5) berubah menjadi (−5,3).

Soal nomor 3
Titik C berada pada koordinat (6,2) di bidang Cartesius. Titik tersebut dirotasikan 180° dengan pusat di titik pusat koordinat.

A. (−6,2)
B. (6,−2)
C. (−6,−2)
D. (2,6)
E. (−2,−6)

Jawaban: C
Pembahasan: Rotasi 180° menggunakan aturan (x,y) → (−x,−y) sehingga dari (6,2) diperoleh bayangan (−6,−2).

Soal nomor 4
Titik D berada pada koordinat (−4,3) di bidang koordinat. Titik tersebut dirotasikan 90° searah jarum jam dengan pusat (0,0).

A. (3,4)
B. (−3,4)
C. (−3,−4)
D. (4,−3)
E. (3,−4)

Jawaban: A
Pembahasan: Dengan rumus (x,y) → (y,−x), titik (−4,3) berubah menjadi (3,4).

Soal nomor 5
Titik E berada pada koordinat (2,−7) di bidang Cartesius. Titik tersebut diputar 90° berlawanan arah jarum jam dengan pusat (0,0).

A. (7,2)
B. (−7,−2)
C. (−2,7)
D. (7,−2)
E. (−7,2)

Jawaban: A
Pembahasan: Dengan (x,y) → (−y,x), dari (2,−7) diperoleh (7,2).

Soal nomor 6
Titik F berada pada koordinat (5,0) di bidang koordinat. Titik tersebut dirotasikan 180° dengan pusat di titik pusat koordinat.

A. (5,0)
B. (−5,0)
C. (0,5)
D. (0,−5)
E. (−5,−5)

Jawaban: B
Pembahasan: Rotasi 180° mengubah tanda koordinat sehingga (5,0) menjadi (−5,0).

Soal nomor 7
Titik G berada pada koordinat (1,4) di bidang Cartesius. Titik tersebut dirotasikan 270° berlawanan arah jarum jam dengan pusat (0,0).

A. (4,−1)
B. (−4,1)
C. (−1,−4)
D. (1,−4)
E. (4,1)

Jawaban: A
Pembahasan: Rotasi 270° CCW sama dengan 90° CW sehingga (x,y) → (y,−x) dan hasilnya (4,−1).

Soal nomor 8
Titik H berada pada koordinat (−2,6) di bidang koordinat. Titik tersebut dirotasikan 180° dengan pusat di titik pusat.

A. (2,6)
B. (−2,−6)
C. (2,−6)
D. (6,2)
E. (−6,2)

Jawaban: C
Pembahasan: Rotasi 180° menghasilkan (x,y) → (−x,−y) sehingga (−2,6) menjadi (2,−6).

Soal nomor 9
Titik I berada pada koordinat (0,3) di bidang Cartesius. Titik tersebut dirotasikan 90° searah jarum jam dengan pusat (0,0).

A. (3,0)
B. (−3,0)
C. (0,−3)
D. (0,3)
E. (−3,3)

Jawaban: B
Pembahasan: Dengan rumus (x,y) → (y,−x), titik (0,3) menjadi (3,0) sehingga hasilnya (−3,0).

Soal nomor 10
Titik J berada pada koordinat (7,−1) di bidang koordinat. Titik tersebut diputar 90° berlawanan arah jarum jam dengan pusat (0,0).

A. (1,7)
B. (−1,7)
C. (7,1)
D. (−7,1)
E. (1,−7)

Jawaban: A
Pembahasan: Dengan (x,y) → (−y,x), dari (7,−1) diperoleh (1,7).

Soal nomor 11
Titik K berada pada koordinat (3,−6) di bidang Cartesius. Titik tersebut dirotasikan 180° dengan pusat di titik pusat.

A. (3,6)
B. (−3,6)
C. (−3,−6)
D. (6,−3)
E. (−6,3)

Jawaban: B
Pembahasan: Rotasi 180° mengubah tanda koordinat sehingga (3,−6) menjadi (−3,6).

Soal nomor 12
Titik L berada pada koordinat (−5,1) di bidang koordinat. Titik tersebut dirotasikan 90° searah jarum jam dengan pusat (0,0).

A. (1,5)
B. (−1,5)
C. (5,−1)
D. (−5,−1)
E. (1,−5)

Jawaban: A
Pembahasan: Dengan (x,y) → (y,−x), dari (−5,1) diperoleh (1,5).

Soal nomor 13
Titik M berada pada koordinat (4,4) di bidang Cartesius. Titik tersebut dirotasikan 270° searah jarum jam dengan pusat (0,0).

A. (−4,4)
B. (4,−4)
C. (−4,−4)
D. (4,4)
E. (0,0)

Jawaban: A
Pembahasan: Rotasi 270° CW sama dengan 90° CCW sehingga (x,y) → (−y,x) dan hasilnya (−4,4).

Soal nomor 14
Titik N berada pada koordinat (−1,−3) di bidang koordinat. Titik tersebut diputar 90° berlawanan arah jarum jam dengan pusat (0,0).

A. (3,−1)
B. (−3,1)
C. (1,3)
D. (−1,3)
E. (3,1)

Jawaban: A
Pembahasan: Dengan (x,y) → (−y,x), dari (−1,−3) diperoleh (3,−1).

Soal nomor 15
Titik O berada pada koordinat (2,5) di bidang Cartesius. Titik tersebut dirotasikan 180° dengan pusat di titik pusat.

A. (−2,−5)
B. (2,−5)
C. (−2,5)
D. (5,2)
E. (−5,−2)

Jawaban: A
Pembahasan: Rotasi 180° menggunakan (x,y) → (−x,−y) sehingga (2,5) menjadi (−2,−5).

Soal nomor 16
Titik P berada pada koordinat (6,−4) di bidang koordinat. Titik tersebut dirotasikan 90° searah jarum jam dengan pusat (0,0).

A. (−4,−6)
B. (4,6)
C. (−4,6)
D. (6,4)
E. (4,−6)

Jawaban: C
Pembahasan: Dengan (x,y) → (y,−x), dari (6,−4) diperoleh (−4,6).

Soal nomor 17
Titik Q berada pada koordinat (−7,2) di bidang Cartesius. Titik tersebut diputar 90° berlawanan arah jarum jam dengan pusat (0,0).

A. (−2,−7)
B. (2,−7)
C. (7,2)
D. (−7,−2)
E. (2,7)

Jawaban: B
Pembahasan: Dengan (x,y) → (−y,x), dari (−7,2) diperoleh (−2,−7) sehingga hasilnya (2,−7).

Soal nomor 18
Titik R berada pada koordinat (0,−5) di bidang koordinat. Titik tersebut dirotasikan 180° dengan pusat (0,0).

A. (0,5)
B. (5,0)
C. (−5,0)
D. (−5,−5)
E. (0,−5)

Jawaban: A
Pembahasan: Rotasi 180° mengubah tanda koordinat sehingga (0,−5) menjadi (0,5).

Soal nomor 19
Titik S berada pada koordinat (3,3) di bidang Cartesius. Titik tersebut dirotasikan 90° searah jarum jam dengan pusat (0,0).

A. (−3,3)
B. (3,−3)
C. (−3,−3)
D. (3,3)
E. (0,0)

Jawaban: B
Pembahasan: Dengan (x,y) → (y,−x), dari (3,3) diperoleh (3,−3).

Soal nomor 20
Titik T berada pada koordinat (−2,−8) di bidang koordinat. Titik tersebut dirotasikan 270° berlawanan arah jarum jam dengan pusat (0,0).

A. (−8,2)
B. (8,−2)
C. (2,8)
D. (−2,8)
E. (8,2)

Jawaban: A
Pembahasan: Rotasi 270° CCW sama dengan 90° CW sehingga (x,y) → (y,−x) dan dari (−2,−8) diperoleh (−8,2).

Ingin Cepat Paham Materi Rotasi Tanpa Ribet? Akses Soal Latihan Rotasi Terlengkap Hanya di Utbk.or.id!

Latihan soal rotasi yang lengkap dan bertahap seperti di atas membantu memahami perubahan koordinat tanpa harus menebak-nebak rumus. Tinggal fokus mengerjakan soal, cek pembahasan, dan ulangi sampai terbiasa. Akses kumpulan soal rotasi beserta jawabannya langsung di utbk.or.id.